Materi ajar : Senin, 17 November 2025

Hari / Tanggal       : Senin 17 november 2025

Fase/Kelas              : C / VI

Mata Pelajaran      : Matematika, Bahasa Indonesia.

Matematika

Pada akhir fase C, peserta didik dapat menunjukkan pemahaman dan intuisi bilangan (number sense) pada bilangan cacah sampai 1.000.000. Mereka dapat membaca, menulis, menentukan nilai tempat, membandingkan, mengurutkan, melakukan komposisi dan dekomposisi bilangan tersebut. Mereka juga dapat menyelesaikan masalah yang berkaitan dengan uang. Mereka dapat melakukan operasi penjumlahan, pengurangan, perkalian, dan pembagian bilangan cacah sampai 100.000. Mereka juga dapat menyelesaikan masalah yang berkaitan dengan KPK dan FPB. Peserta didik dapat membandingkan dan mengurutkan berbagai pecahan termasuk pecahan campuran, melakukan operasi penjumlahan dan pengurangan pecahan, serta melakukan operasi perkalian dan pembagian pecahan dengan bilangan asli. Mereka dapat mengubah pecahan menjadi desimal, serta membandingkan dan mengurutkan bilangan desimal (satu angka di belakang koma)

Tujuan Pembelajaran : Murid dapat memahami cara membaca Rasia bilangan dengan baik. 

Bahasa Indonesia

Capaian Pembelajaran: 

Murid mampu menganalisis informasi dan nilai-nilai dari teks sastra (legenda) dan informasional (catatan perjalanan, teks museum). Murid mampu menemukan dan mengidentifikasi informasi pada fitur grafis (grafik), serta menulis teks laporan untuk menjelaskan hasil pengamatan

Tujuan Pembelajaran: 

Murid dapat :

1. Memahami isi legenda "Putri Komodo" dan mengidentifikasi majas yang digunakan.

2. Menganalisis catatan perjalanan untuk membedakan informasi yang bersifat fakta dan opini.

3. Mengubah kalimat langsung menjadi kalimat tidak langsung (dan sebaliknya) sesuai konteks.

4. Menganalisis data dari grafik dan menyajikannya kembali dalam bentuk kalimat informatif.

5. Menulis laporan hasil pengamatan/kunjungan ke museum atau tempat bersejarah dengan struktur yang baik

Assalamu'alaikum warohmatullah wabarokatuh

Apa kabar anak sholih sholihah
Semoga semuanya dalam keadaan sehat wal'aafiyat
Jangan lupa sarapan dan persiapkan buku pelajaran kalian ya...
Mari awali kegiatan belajar hari ini dengan berdoa.

BAHASA INDONESIA

BAHASA INDONESIA

FAKTA DAN OPINI

Pada pembelajaran Bahasa Indonesia kelas VI Kurikulum Merdeka terdapat pembahasan tentang Fakta dan Opini Teks “Taman Nasional Tanjung Puting”. Tujuan pembelajaran kali ini adalah Ppeserta didik memahami inti dari catatan perjalanan dengan menjawab pertanyaan, membedakan opini dan fakta, dan mencari makna dari kosakata baru.

Pada kegiatan ini peserta didik menjelaskan ide pokok dan banyak ide pendukung dari sebuah teks sastra dan informasional yang terus meningkat sesuai jenjangnya. Mengidentifikasi dan memahami kata-kata yang memiliki makna jamak yang sering digunakan sehari-hari (misalnya keberagaman, warisan) dan kata-kata baru (misalnya globalisasi) pada teks sesuai jenjangnya dengan menggunakan petunjuk visual dan konteks kalimat yang mendukung.

Fakta adalah keadaan atau peristiwa yang benar-benar ada atau terjadi dalam kehidupan nyata. Kebenaran yang dikandung dalam fakta ini sudah terbukti dan terverifikasi. Oleh karena itu saat dihadapkan dengan fakta, tidak ada orang yang bisa membantahnya. Misalnya, ketika seseorang mengatakan bahwa matahari terbit dari timur, kita tidak bisa membantahnya karena hal itu benar-benar terjadi.

Berbeda dengan kalimat fakta yang mengandung kebenaran yang sudah terbukti, kebenaran dalam opini belum terbukti, karena kalimat opini mengandung pendapat, pandangan, gagasan, sikap, saran atau solusi penulis terhadap sebuah masalah atau kejadian yang sedang dibahas dalam artikelnya. Sekalipun demikian, bila sebuah opini pada akhirnya terbukti kebenarannya, maka opini tersebut berubah menjadi fakta.

Apakah kalian suka catatan perjalanan itu? Sekarang, jawablah pertanyaan-pertanyaan ini, ya!

1. Mengapa penulis sangat ingin mengunjungi Taman Nasional Tanjung Puting?

Penulis ingin mengunjungi Taman Nasional Tanjung Puting karena pernah membaca tentang peneliti yang mengadvokasi pelestarian orang utan dan hutan hujan tropis.

2. Mengapa penulis mengatakan bahwa perjalanannya istimewa? Jelaskan dengan kata-katamu sendiri!

Perjalanan tersebut istimewa karena mereka tidak menginap di penginapan, tetapi di rumah perahu yang disebut kelotok.

3. Kegiatan apa saja yang dilakukan oleh pusat rehabilitasi orang utan?

Kegiatan pusat rehabilitasi orang utan antara lain merawat orang utan yang menjadi korban kejahatan (misalnya dengan memberi makan) dan kemudian melepaskan mereka kembali ke habitat aslinya.

Mengelompokkan Informasi

Supaya lebih memahami suatu teks atau wacana, kalian bisa mengelompokkan informasi yang terdapat di dalamnya. Pengelompokan bisa dilakukan berdasar kejadian kronologis, atau berdasar tempat kejadiannya. Pengelompokan ini juga akan membantu kalian memahami bacaan. Coba lengkapi tabel di bawah ini dengan informasi yang kalian dapatkan dari catatan perjalanan di halaman sebelumnya. 

Hari Ke	Tempat	Informasi atau Peristiwa Penting
1.	Tanjung Harapan	Bertemu Gundul dan orang utan lain di tempat pemberian makan. Melihat Bekantan.  Makan malam dengan kunang-kunang
1.	Tanjung Puting	Melihat bekantan Melihat burung Rangkong
2.	Pondok Tanggul	Melihat orang utan bersantai di pohon: Rini dan dua bayinya bernama Ricak dan Robby.  Tidak ada orang utan yang datang saat pemberian makanan
2.	Camp Leakey	Adik penulis mengeluh capek ketika harus berjalan dari dermaga ke tempat pemberian makan.  Bertemu dengan Tom, orang utan yang dikenal sebagai penguasa hutan.  Mengunjungi pusat informasi tentang orang utan.  97% DNA oramg utan sama dengan DNA manusia.  Melihat rumah Prof. Birute Galdikas, orang yang pertama kali meneliti orang utan di Tanjung Puting.  Melihat gerhana bulan dari dek kelotok
3.	Desa Sekonyer	Melihat-lihat desa tempat bermukimnya penduduk yang sebelumnya tinggal di dalam taman nasional.  Di sini turis dapat membeli kerajinan tangan hasil karya penduduk.

Opini atau Fakta

Baca dengan saksama pernyataan dari catatan perjalanan di atas dan tentukan apakah kalimat tersebut opini atau fakta. Beri tanda centang di kolom yang sesuai.

No.	Pernyataan	Opini	Fakta
1.	Perjalanan ini istimewa karena kami menginap di rumah perahu atau kelotok.	✓	-
2.	Tom, orang utan di Camp Leakey, memiliki kekuatan setara delapan orang dewasa.	-	✓
3.	Prof. Birute Galdikas pertama kali meneliti orang utan di Tanjung Puting pada tahun 1971.	-	✓
4.	Pemandangan malam di hutan tampak indah.	✓	-
5.	Penduduk Desa Sekonyer awalnya tinggal di dalam taman nasional, tapi kemudian dipindah ke lokasi ini.tanda	-	✓

Kosakata Baru dalam Bacaan “Bertemu Orang Utan”

1. taman nasional: kawasan pelestarian alam yang dikelola, dimanfaatkan untuk kegiatan ilmu pengetahuan, pendidikan dan pelatihan, serta rekreasi dan pariwisata
2. kelotok: n perahu bermotor (di daerah Kalimantan Selatan) terbuat dari kayu untuk kendaraan sungai
3. dermaga: n tembok rendah yang memanjang di tepi pantai menjorok ke laut di kawasan pelabuhan (untuk pangkalan dan bongkar muat barang); kade
4. mengadvokasi: melakukan pembelaan
5. tanah gambut: Tan tanah yang terbentuk dari proses pelapukan tumbuhan rawa, kurang subur
6. pemandu wisata: orang yang pekerjaannya mendampingi wisatawan dengan mengatur perjalanan dan memberi penjelasan tentang tempat yang dikunjungi; orang yang bertugas memandu wisatawan; pramuwisata
7. habitat: n Bio tempat hidup organisme tertentu; tempat hidup yang alami (bagi tumbuhan dan hewan); lingkungan kehidupan asli, n Geo tempat kediaman atau kehidupan tumbuhan, hewan, dan manusia dengan kondisi tertentu pada permukaan bumi
8. polusi cahaya: lampu dan cahaya buatan yang membuat langit terlalu terang sehingga bintang tidak terlihat
9. endemik: berkenaan dengan spesies organisme yang terbatas pada wilayah  geografis tertentu

Demikian pembahasan mengenai Fakta dan Opini Teks “Taman Nasional Tanjung Puting” Semoga tulisan ini bermanfaat.

Sumber : Buku Bahasa Indonesia Kelas VI Kurikulum Merdeka, Kemendikbud

Kamu pernah main rubik nggak? Itu looh, permainan teka-teki dengan menyusun warna-warna kotak menjadi selaras/sama di setiap sisinya. Kalo kamu pernah main, bentuk rubik ini unik, ya. Bentuknya kotak yang tersusun oleh kotak-kotak kecil warna-warni. Nah, permainan ini merupakan contoh nyata dari bangun ruang, tepatnya bangun ruang kubus.

Gambar Rubik

 

Pada artikel kali ini, kita akan membahas lebih jauh tentang bangun ruang, mulai dari pengertian, ciri-ciri, hingga rumus dan contoh soalnya. Langsung aja kita bahas, yuk!

 

Apa itu Bangun Ruang?

Bangun ruang adalah bentuk yang memiliki panjang, lebar, dan tinggi. Bangun ruang berbeda dengan bangun datar yang hanya memiliki panjang dan lebar aja. Bangun ruang berbentuk tiga dimensi (3D), sementara bangun datar berbentuk dua dimensi (2D).

Baca Juga: Rumus Bangun Datar (Luas dan Keliling) serta Contohnya

Pada bangun ruang, kita bisa mencari luas permukaan dan volume. Wah, apa itu volume? Volume adalah kapasitas atau penghitungan seberapa banyak ruang yang bisa ditempati/diisi oleh suatu objek.

Misalnya seperti saat kita mengisi botol air minum. Biasanya kan, botol air minum memiliki ukuran kapasitas yang tertera di bagian bawah botol, seperti 500 ml, 700 ml, atau 1 liter. Nah, kapasitas inilah yang dinamakan volume. Jika suatu botol air minum tertulis memiliki volume 1 liter, maka jumlah maksimal air minum yang dapat ditampung oleh botol tersebut adalah sebanyak 1 liter.

Gimana, paham ya?

Sementara itu, luas permukaan adalah jumlah luas dari semua sisi yang menutupi bagian luar dari suatu bangun ruang. Luas permukaan berguna saat kita ingin membuat jaring-jaring sebuah bangun ruang.

Ilustrasi menuang air ke dalam botol. (Sumber: Giphy.com)

 

Contoh bangun ruang juga ada banyak di sekitar kita, loh. Berdasarkan bentuknya, bangun dibagi menjadi dua jenis, yaitu bangun ruang sisi lengkung dan bangun ruang sisi datar.

Sesuai namanya, bangun ruang sisi lengkung memiliki sisi yang berbentuk melengkung. Contohnya seperti tabung, kerucut, dan bola. Sedangkan bangun ruang sisi datar memiliki sisi yang berbentuk datar. Contohnya seperti kubus, balok, limas, dan prisma. 

 

Ciri-Ciri Bangun Ruang

Secara umum, ciri-ciri atau sifat-sifat bangun ruang adalah sebagai berikut:

• Memiliki wajah atau sisi permukaan
• Memiliki tepi atau rusuk (tempat bertemunya sisi dengan sisi lainnya)
• Memiliki sudut
• Memiliki volume

 

Ciri yang disebut di atas juga dapat disebut sebagai unsur-unsur bangun ruang, atau karakteristik yang harus dimiliki suatu bangun untuk dapat disebut sebagai bangun ruang.

Baca Juga: Kedudukan Titik, Garis, dan Bidang pada Bangun Ruang

 

Rumus Luas dan Volume Bangun Ruang

Berikut rumus-rumus bangun ruang berdasarkan masing-masing jenisnya. Simak baik-baik, ya!

 

1. Rumus Luas dan Volume Kubus

Kubus adalah bangun ruang yang memiliki enam sisi berbentuk persegi yang sama besar. Semua rusuk pada kubus memiliki panjang yang sama.

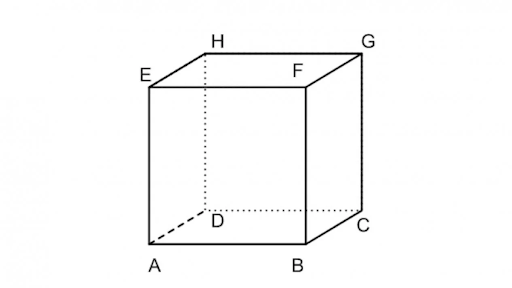
Gambar Kubus (Sumber: thumb.viva.co.id)

 

Ciri-Ciri Kubus

• Memiliki 12 rusuk yang panjang sama.
• Memiliki 6 sisi berbentuk persegi.
• Memiliki 8 titik sudut.
• Memiliki 12 diagonal sisi atau diagonal bidang.
• Memiliki 4 diagonal ruang.
• Memiliki 6 bidang diagonal.
• Memiliki 3 pasang bidang sejajar yang sama dan sebangun.

 

Rumus Luas Permukaan Kubus

Luas Permukaan = 6 × sisi × sisi 

L = 6 × s2

 

Rumus Volume Kubus

Volume = sisi × sisi × sisi 

V = s3

 

Contoh Soal:

Sebuah kubus memiliki panjang sisi 4 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui: s = 4 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan kubus

L = 6 × s2

L = 6 × 42

L = 6 × 16 = 96 cm²

Jadi, luas permukaan kubus tersebut adalah 96 cm².

 

b. Volume kubus

V = s3

V = 43

V = 64 cm³

Jadi, volume kubus tersebut adalah 64 cm³.

 

2. Rumus Luas dan Volume Balok

Sama seperti kubus, balok adalah bangun ruang yang memiliki enam sisi, namun sisi-sisinya berbentuk persegi panjang. Tiga pasang sisi balok yang berhadapan akan sama besar.

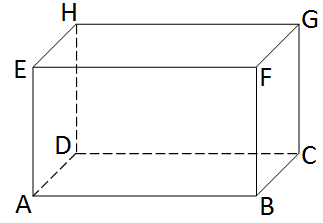
Gambar Balok (Sumber: Ruangguru.com)

 

Ciri-Ciri Balok

• Memiliki 6 buah sisi.
• Memiliki 12 rusuk.
• Memiliki 12 diagonal bidang.
• Memiliki 8 titik sudut.
• Memiliki 4 diagonal ruang.
• Memiliki 6 bidang diagonal.
• Memiliki luas permukaan dan volume.

 

Rumus Luas Permukaan Balok

Luas Permukaan = 2 × ((panjang × lebar) + (panjang × tinggi) + (lebar × tinggi))

L = 2 × ((p × l) + (p × t) + (l × t))

 

Rumus Volume Balok

Volume = panjang × lebar × tinggi

V = p × l × t

 

Contoh Soal:

Sebuah balok memiliki panjang 8 cm, lebar 4 cm, dan tinggi 6 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui: p = 8 cm, l = 4 cm, t = 6 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan balok

L = 2 × ((p × l) + (p × t) + (l × t))

L = 2 × ((8 × 4) + (8 × 6) + (4 × 6)) 

L = 2 × (32 + 48 + 24) = 208 cm²

Jadi, luas permukaan balok tersebut adalah 208 cm².

 

b. Volume balok

V = p × l × t

V = 8 × 4 × 6 = 192 cm³

Jadi, volume balok tersebut adalah 192 cm³.

Baca Juga: Macam-Macam, Sifat & Rumus Bangun Segi Empat 

 

3. Rumus Luas dan Volume Limas

Selanjutnya, limas adalah bangun ruang yang memiliki alas berbentuk segitiga, segiempat, segilima, segienam, dan seterusnya (segi-n), dan sisi-sisi tegak berbentuk segitiga yang bertemu di satu titik puncak.

Jika alas limas berbentuk segitiga, maka bangun tersebut disebut limas segitiga. Jika alasnya berbentuk segiempat, maka disebut limas segiempat, begitupun dengan limas segilima, limas segienam, dan seterusnya.

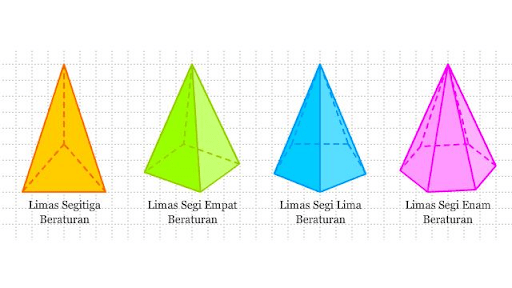
Gambar Limas (Sumber: Popmama.com)

 

Ciri-Ciri Limas

• Memiliki 7 titik sudut.
• Memiliki 12 rusuk.
• Memiliki 6 sisi tegak.
• Memiliki 1 sisi alas.
• Mempunyai sisi tegak berbentuk segitiga.
• Sisi alasnya berbentuk segi banyak.
• Mempunyai satu titik puncak.
• Penamaan limas tergantung bentuk alasnya.

 

Rumus Luas Permukaan Limas

Luas Permukaan = Luas alas + Luas selimut

L = Lalas + Lselimut

 

Rumus Volume Limas

Volume = 1/3 × Luas alas × tinggi limas

V = 1/3 × Lalas × t

 

Keterangan:

• Luas alas limas, rumusnya tergantung pada bentuk alas limas. Misalnya, pada limas segiempat, luas alasnya = p x l.
• Luas selimut​ adalah luas sisi-sisi tegak limas. Karena sisi-sisi tegak limas berbentuk segitiga, maka Lselimut​ = 1/3 × panjang alas × t.

 

Contoh Soal:

Sebuah limas persegi memiliki panjang sisi alas 5 cm dan tinggi 10 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui:

p = 5 cm

t = 10 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan limas

L = Lalas + Lselimut

Kita cari luas alas dan luas selimutnya satu per satu, ya!

• Luas alas

Karena alas limas tersebut berbentuk persegi, jadi untuk mencari luas alas, kita menggunakan rumus mencari luas persegi.

L = s2 = 52 = 25 cm²

• Luas selimut
  

Kemudian, untuk luas selimut, kita bisa gunakan luas segitiga, yaitu:

L = ½ × a × t

L = ½ × 5 × 10 = 25 cm²

Setelah kita mendapatkan luas alas dan luas selimutnya, barulah kita bisa mencari luas permukaan limas.

L = Lalas + Lselimut

L = 25 + 25 = 50 cm²

Jadi, didapat luas permukaan limas persegi tersebut adalah 50 cm².

 

b. Volume limas

V = 1/3 × Lalas × t

V = 1/3 × 25 × 10 = 83,33 cm³

Jadi, volume limas persegi tersebut adalah 83,33 cm³.

 

4. Rumus Luas dan Volume Prisma

Prisma adalah bangun ruang yang memiliki dua alas sejajar dan kongruen, serta sisi tegak yang berbentuk segi empat. Sama seperti limas, prisma diberi nama berdasarkan bentuk alasnya. Kalo alasnya berbentuk segitiga, maka namanya prisma segitiga, begitupun seterusnya.

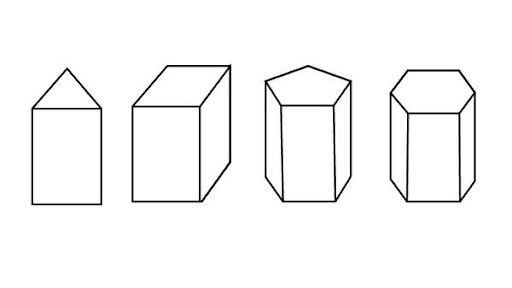
Gambar Prisma (Sumber: Popmama.com)

 

Ciri-Ciri Prisma

• Memiliki alas, tutup, dan selimut.
• Selimut prisma merupakan bidang datar, bisa kotak ataupun persegi panjang.
• Memiliki sudut sebanyak 2 kali segi alasnya.
• Memiliki rusuk 3 kali segi alasnya.
• Memiliki ujung-ujung yang identik satu sama lain.

 

Rumus Luas Permukaan Prisma

Luas Permukaan = (2 × Luas alas) + Luas selimut

L = (2 × Lalas) + Lselimut

L = (2 × Lalas) + (Kalas × t)

 

Rumus Volume Prisma

Volume = Luas alas × tinggi prisma

V = Lalas × t

Keterangan:

• Luas alas prisma, rumusnya tergantung pada bentuk alas prisma. Misalnya, pada prisma segiempat, luas alasnya = p x l.
• Luas selimut​ adalah luas sisi-sisi tegak prisma. Kita bisa mencarinya dengan rumus keliling alas × tinggi.
• Rumus volume prisma segiempat maupun segi lainnya, dihitung menggunakan rumus volume prisma secara umum.

 

Contoh Soal:

1. Sebuah prisma segitiga siku-siku memiliki panjang sisi alasnya 3 cm, 4 cm, dan 5 cm. Jika tinggi prisma adalah 6 cm, berapakah luas permukaan prisma tersebut?

 

Pembahasan:

L = (2 × Lalas) + (Kalas × t)

Kita cari luas alas dan keliling alasnya dulu, ya. Karena alas prisma berbentuk segitiga siku-siku, maka luas alasnya bisa kita cari menggunakan rumus:

L = ½ × a × t

L = ½ × 3 × 4 = 6 cm²

Kemudian, untuk keliling alas, kita bisa cari dengan menghitung jumlah sisi-sisi segitiga:

Kalas = sisi + sisi + sisi = 3 + 4 + 5 = 12 cm

Sehingga, luas permukaan prismanya adalah:

L = (2 × Lalas) + (Kalas × t)

L = (2 × 6) + (12 × 6)

L = 12 + 72 = 84 cm²

Jadi, luas permukaan prisma segitiga tersebut adalah 84 cm².

 

2. Sebuah prisma segitiga memiliki luas alas 20 cm² dan tinggi prisma 12 cm. Hitunglah volumenya!

 

Pembahasan:

V = Lalas × t

V = 20 × 12 = 240 cm³

Jadi, volume prisma segitiga tersebut adalah 240 cm³.

Baca Juga: Cara Menghitung Luas Permukaan dan Volume Gabungan Bangun Ruang Sisi Lengkung

 

5. Rumus Luas dan Volume Bola

Bola adalah bangun ruang yang seluruh permukaannya berjarak sama dari titik pusatnya. Karena termasuk bangun ruang sisi lengkung, maka bola tidak memiliki sisi datar.

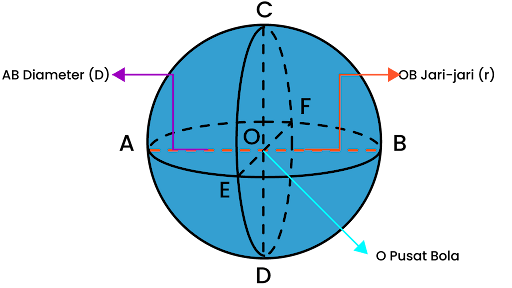
Gambar Bola (Sumber: Ruangguru.com)

 

Ciri-Ciri Bola

• Tidak memiliki rusuk dan titik sudut.
• Memiliki satu bidang sisi lengkung, yakni selimut bola.
• Terdapat jari-jari dan diameter.
• Memiliki luas permukaan dan volume.

 

Rumus Luas Permukaan Bola

Luas Permukaan = 4 × π × (jari-jari bola)2

L = 4 × π × r2

 

Rumus Volume Bola

Volume = 4/3 × π × (jari-jari bola)3

V = 4/3 × π × r3

 

Rumus Volume Setengah Bola

Volume = 2/3 × π × jari-jari bola

V = 2/3 × π × r

 

Catatan: Nilai π bisa 22/7 atau 3,14, tergantung yang diketahui di soal.

 

Contoh Soal:

Sebuah bola memiliki jari-jari 7 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

a. Luas permukaan bola

L = 4 × π × r2

L = 4 × 22/7 × 72 

L = 4 × 22/7 × 49 = 616 cm²

Jadi, luas permukaan bola tersebut adalah 616 cm².

 

b. Volume bola

V = 4/3 × π × r3

V = 4/3 × 22/7 × 73 

V = 4/3 × 22/7 × 343 = 1.436 cm³

Jadi, volume bola tersebut adalah 1.436 cm³.

Baca Juga: Rumus Luas dan Volume Bola, Cara Menghitung & Contohnya

 

6. Rumus Luas dan Volume Kerucut

Kamu pernah menggunakan topi ulang tahun? Nah, topi ulang tahun itu bentuknya seperti kerucut, loh. Secara definisi, kerucut adalah bangun ruang yang memiliki alas berbentuk lingkaran dan sisi tegak yang melengkung dan bertemu di satu titik puncak.

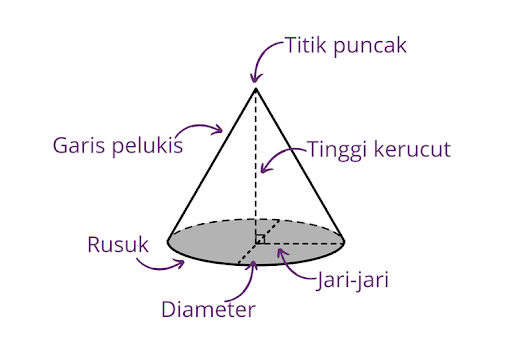
Gambar Kerucut (Sumber: Kompas.com)

 

Ciri-Ciri Kerucut

• Mempunyai 2 sisi berbentuk lingkaran dan melengkung.
• Sisi lingkaran merupakan alas, dan sisi melengkung sebagai selimut.
• Mempunyai 1 rusuk berbentuk bulat.
• Mempunyai 1 sudut di ujung kerucut.

 

Rumus Luas Permukaan Kerucut

Luas Permukaan = π × jari-jari alas × (jari-jari alas + garis pelukis)

L = π × r × (r + s)

 

Rumus Volume Kerucut

Volume = 1/3 × π × (jari-jari alas)2 × tinggi kerucut

V = 1/3 × π × r2 × t

 

Rumus Garis Pelukis Kerucut

 

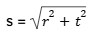
Contoh Soal:

Sebuah kerucut memiliki jari-jari alas 5 cm dan tinggi 12 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui:

r = 5 cm

t = 12 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan kerucut

L = π × r × (r + s)

Pertama-tama, kita cari garis pelukis kerucutnya terlebih dahulu, ya:

Sehingga, garis pelukis kerucut tersebut adalah 13 cm. Dengan begitu, kita bisa mencari luas kerucutnya dengan cara:

L = π  ×  r  ×  (r  +  s)

L = 22/7 × 5 × (5 + 13) 

L = 22/7 × 5 × 18 = 282,74 cm²

Jadi, luas permukaan kerucut tersebut adalah 282,74 cm².

 

b. Volume kerucut

V = 1/3 ×  π  ×  r2 × t

V = 1/3 × 22/7 × 52 × 12 = 314 cm³

Jadi, volume kerucut tersebut adalah 314 cm³.

Baca Juga: Rumus Luas & Volume Kerucut serta Contoh Soalnya

 

7. Rumus Luas dan Volume Tabung

Kalo ngomongin tabung, pasti banyak di antara kamu yang udah kebayang bentuknya, ya. Tabung adalah bangun ruang yang memiliki alas dan tutup berbentuk lingkaran yang sama besar, serta sisi tegak yang berbentuk persegi panjang melingkar. Contohnya kayak dirigen minyak, nih.

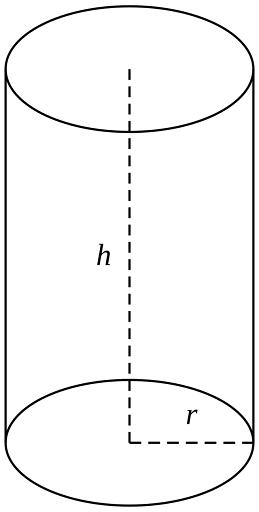
Gambar Tabung (Sumber: Wikimedia.org)

 

Ciri-Ciri Tabung

• Memiliki 2 rusuk.
• Memiliki 3 sisi, yaitu 2 sisi berbentuk lingkaran dan 1 sisi lengkung.
• Tinggi tabung adalah jarak antara alas dengan tutup tabung.
• Sisi alas serta tutupnya berbentuk lingkaran dan sama besar.
• Tidak memiliki titik sudut.

 

Rumus Luas Permukaan Tabung

Luas Permukaan = 2 × π × jari-jari alas × (jari-jari alas + tinggi tabung)

L = 2 × π × r × (r + t)

 

Rumus Volume Tabung

Volume = π × (jari-jari alas)2 × tinggi tabung

V = π × r2 × t

 

Contoh Soal:

Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 10 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui:

r = 7 cm

t = 10 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan tabung

L = 2 × π × r × (r + t)

L = 2 × 22/7 × 7 × (7 + 10) 

L = 2 × 22/7 × 7 × 17  = 748 cm²

Jadi, luas permukaan tabung tersebut adalah 748 cm².

 

b. Volume tabung

V = π × r2 × t

V = 22/7 × 72 × 10

V = 22/7 × 49 × 10 = 1.540 cm³

Jadi, volume tabung tersebut adalah 1.540